Where Math meets Music

Ever wonder why some note combinations sound pleasing to our ears, while others make us cringe? To understand the answer to this question, you’ll first need to understand the wave patterns created by a musical instrument. When you pluck a string on a guitar, it vibrates back and forth. This causes mechanical energy to travel through the air, in waves. The number of times per second these waves hit our ear is called the ‘frequency’. This is measured in Hertz (abbreviated Hz). The more waves per second the higher the pitch. For instance, the A note below middle C is at 220 Hz. Middle C is at about 262 Hz.

Now, to understand why some note combinations sound better, let’s first look at the wave patterns of 2 notes that sound good together. Let’s use middle C and the G just above it as an example:

Now let’s look at two notes that sound terrible together, C and F#:

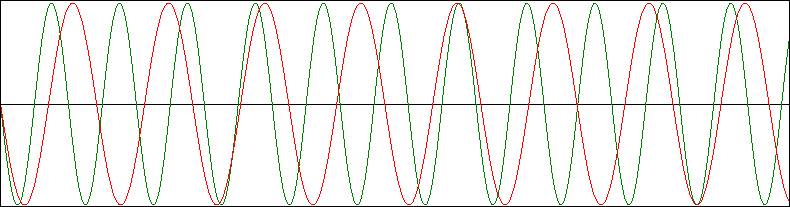
Do you notice the difference between these two? Why is the first ‘consonant’ and the second ‘dissonant’? Notice how in the first graphic there is a repeating pattern: every 3^rd wave of the G matches up with every 2^nd wave of the C (and in the second graphic how there is no pattern). This is the secret for creating pleasing sounding note combinations: Frequencies that match up at regular intervals (* - Please see footnote about complications to this rule).

Now let’s look at a chord, to find out why it’s notes sound good together. Here are the frequencies of the notes in the C Major chord (starting at middle C):

            C – 261.6 Hz
            E – 329.6 Hz
            G – 392.0 Hz

The ratio of E to C is about 5/4ths. This means that every 5^th wave of the E matches up with every 4^th wave of the C. The ratio of G to E is about 5/4ths as well. The ratio of G to C is about 3/2. Since every note’s frequency matches up well with every other note’s frequencies (at regular intervals) they all sound good together!

Now let’s look at the ratios of the notes in the C Major key in relation to C:

C – 1
D – 9/8
E – 5/4
F – 4/3
G – 3/2
A – 5/3
B – 17/9

To tell you the truth, these are approximate ratios. Remember when I said the ratio of E to C is about 5/4ths? The actual ratio is not 1.25 (5/4ths) but 1.2599. Why isn’t this ratio perfect? That’s a good question. When the 12-note ‘western-style’ scale was created, they wanted not only the ratios to be in tune, but they also wanted the notes to go up in equal sized jumps. Since they couldn’t have both at the same time, they settled on a compromise. Here are the actual frequencies for the notes in the C Major Key:

Note	Perfect Ratio to C	Actual Ratio to C	Ratio off by	Frequency in Hz
Middle C				261.6
D	9/8 or 1.125	1.1224	0.0026	293.7
E	5/4 or 1.25	1.2599	0.0099	329.6
F	4/3 or 1.333…	1.3348	0.0015	349.2
G	3/2 or 1.5	1.4983	0.0017	392.0
A	5/3 or 1.666…	1.6818	0.0152	440.0
B	17/9 or 1.888…	1.8877	0.0003	493.9

You can see that the ratios are not perfect, but pretty close. The biggest difference is in the C to A ratio. If the ratio was perfect, the frequency of the A above middle C would be 436.04 Hz, which is off from 'equal temperament' by about 3.96 Hz.

The previous list shows only the 7 notes in the C Major key, not all 12 notes in the octave. Each note in the 12 note scale goes up an equal amount, that is, an equal amount exponentially speaking.

Here is the equation to figure out the Hz of a note:

Hertz (number of vibrations a second) = 6.875 x 2 ^ ( ( 3 + MIDI_Pitch ) / 12 )

The ^ symbol means ‘to the power of’. The MIDI_Pitch value is according to the MIDI standard, where middle C equals 60, and the C an octave below it equals 48. As an example, let’s figure the hertz for middle C:

Hertz = 6.875 x 2 ^ ( ( 3 + 60 ) / 12 ) = 6.875 x 2 ^ 5.25 = 261.6255

The next note up, C#, is:

Hertz = 6.875 x 2 ^ ( ( 3 + 61 ) / 12 ) = 277.1826

And the next note, D, is:

Hertz = 6.875 x 2 ^ ( ( 3 + 62 ) / 12 ) = 293.6648

The jump between C and C# is 15.56 Hertz, the jump between C# and D is 16.48 Hertz. Although the Hertz jump is not equal between the notes, it is an equal jump in the exponent number and it sounds like an equal jump to our ears going up the scale. This gives a nice smooth transition going up the scale.

Another important feature of the scale is that it jumps by 2 times each octave. The A below middle C is at 220 Hertz, the A above middle C is at 440 Hertz, and the A above that is at 880 Hertz. This means that you can move notes into different octaves and still have them sound consonant. For instance, let’s take the case of middle C and G again, except move G into the next octave. We still have middle C at 261.6Hz, but G is now at 784 Hz. That gives a ratio from G to C of about 3/1 (twice the original ratio of 3/2). The waves still meet up at regular intervals and they still sound consonant! Another nice feature of having an equal exponential jump is that you can start a scale on any note you wish, including the black keys. For instance, instead of C,D,E,F,G,A,B, you can start on, say, D# and have D#,F,G,G#,A#,C,D as your scale with the same great sounding combinations of frequencies.

At a certain point frequency ratios are too great to sound consonant. It takes too many waves for them to match up, and our ears just can’t seem to find a regular pattern. At what point is this? The simple answer is when the ratio’s numerator or denominator gets to about 13. For instance, C# has a frequency ratio to C of about 18/17ths. That’s just too many waves before they meet up, and you can tell that immediately when you play them together.

So now you’re thinking that we have a scale that goes up in even steps and has reasonably accurate ratios, we’re all set, right? Actually, there are a lot of dissenting opinions on the subject. Remember those not-quite-accurate ratios? One reason for this was for instruments to be able to be tuned once, and sound reasonably good in all keys. Some of the grumpier musicians still complain, though, saying that equal temperament makes all keys sound equally bad. If you tune to just one particular key, you can get those ratios perfect (since the human ear can detect a difference of 1Hz, being off by several Hz can be a problem!).

Maybe more importantly, though, is that there are a lot of undiscovered frequency combinations that can’t be played in the confining 12-note system. Many alternative scales used in India have up to 22 notes per octave. If you’re not satisfied with the standard western scale, there are lot of alternative tuning methods available, such as 'Just Intonation' and 'Lucy Tuning'. With modern digital equipment, these alternate tunings have become much easier to implement. We should hear some new and incredibly interesting music come out of these tuning methods as they are gradually accepted into the mainstream.

* - The frequency ratio theory of consonance does not always hold true. See this other article for an explanation.

Here are some links if you’d like to explore this topic further:

Just Intonation Network

Just Intonation explained

Lucy Tuning

Just vs Equal Temperment – ‘harmonic tuning’ described

American Festival of Microtonal Music

Click here to go back to our home page, for info on Music MasterWorks voice-to-note composer and
In-Tune Multi-Instrument Tuner.